LA CALCULADORA DE ALICIA

Pasos de cálculo

Calculadora Alicia online gratis: operaciones matemáticas paso a paso

La Calculadora Alicia es una calculadora online gratuita en español que resuelve operaciones matemáticas paso a paso. Con una interfaz sencilla y didáctica, permite practicar desde sumas, restas, multiplicaciones y divisiones hasta ejercicios más completos como fracciones, raíces cuadradas, números romanos, tablas de multiplicar y notación científica. También incluye funciones de calculadora científica online, ideales para trabajar con ecuaciones, polinomios y factorización. Diseñada para estudiantes de primaria y secundaria, es una herramienta educativa clara, práctica y accesible para docentes y familias.

Origen y visión educativa de la Calculadora Alicia

La historia de la Calculadora Alicia nace de una necesidad pedagógica: simplificar la manera en que los niños aprenden aritmética. El proyecto se inspiró parcialmente en la imagen de ‘Alicia en el país de las maravillas’, una referencia que ayuda a humanizar la herramienta. Detrás de la iniciativa hay docentes y tecnólogos que enfocaron el diseño en la usabilidad, el respeto a la privacidad y la adaptabilidad a distintos niveles. Su visión es ofrecer una calculadora online que no se limite a dar un resultado, sino que muestre el procedimiento, fomente la práctica y explique por qué los pasos funcionan. La calculadora Alicia se creó con la idea de acompañar el aprendizaje desde edades tempranas.

Principales Características y Funciones de la Calculadora Alicia

Operaciones Aritméticas Básicas

La Calculadora Alicia te permite realizar de forma rápida y precisa operaciones aritméticas esenciales como sumas, restas, multiplicaciones y divisiones.
Ya sea que estés resolviendo tareas escolares, calculando tu presupuesto personal o haciendo operaciones diarias, esta herramienta te ofrece resultados exactos en cuestión de segundos.
Solo tienes que ingresar los números, seleccionar la operación y obtener la respuesta inmediata sin complicaciones.

Interfaz Fácil de Usar

Una de las mayores ventajas de la Calculadora Alicia es su diseño limpio e intuitivo.
La disposición de los botones está pensada para que cualquier usuario —desde un estudiante principiante hasta un profesional experimentado— pueda utilizarla sin esfuerzo.
La interfaz es clara, sin distracciones, y con etiquetas visibles que facilitan encontrar rápidamente cada función.

Funciones Matemáticas Avanzadas

Además de las operaciones básicas, la calculadora incluye herramientas avanzadas como el cálculo de raíces cuadradas y la factorización en números primos, útiles tanto para el estudio como para el trabajo técnico.
También admite valores decimales, recordando que para introducir un número decimal se debe usar la coma “,” en lugar del punto “.”
Estas funciones amplían las posibilidades de uso, permitiendo resolver ejercicios más complejos de manera precisa.

Soluciones Paso a Paso

La Calculadora Alicia no se limita a mostrar un resultado: explica el procedimiento completo para llegar a él.
Cada cálculo se acompaña de un desglose paso a paso, lo que la convierte en una herramienta ideal para estudiantes y docentes que desean comprender el proceso matemático detrás de cada operación.
De esta forma, no solo obtienes respuestas, sino también aprendizaje y comprensión.

Modo Oscuro

La Calculadora Alicia ofrece modo oscuro para una experiencia más cómoda y agradable en condiciones de poca luz.
Este modo reduce la fatiga visual y mejora la concentración, manteniendo el mismo nivel de contraste y legibilidad.
Es una función pensada especialmente para quienes trabajan o estudian durante la noche.

Gratuita y Sin Restricciones

La Calculadora Alicia es completamente gratuita.
No requiere registro ni suscripción, y puedes utilizar todas sus funciones sin limitaciones.
De esta manera, tanto estudiantes como profesores y profesionales pueden disfrutar de una calculadora potente y accesible sin preocuparse por costos ocultos.

Guía Paso a Paso para Utilizar la Calculadora Alicia

Sigue estos pasos para aprovechar al máximo todas las funciones de la calculadora:

1. Accede a la Calculadora

Entra en nuestro sitio web y encontrarás la Calculadora Alicia disponible en la parte superior de la página principal, lista para usarse de inmediato.

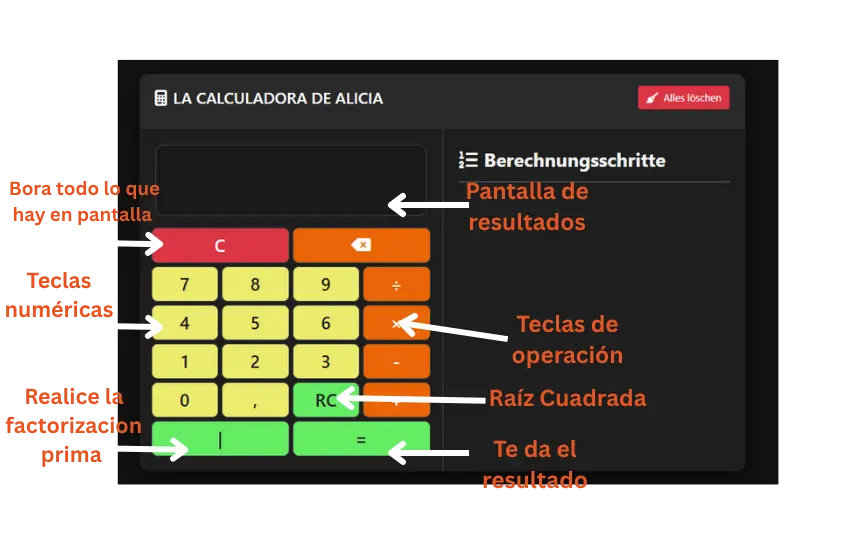
2. Conoce su Diseño

Pantalla de visualización: muestra los números introducidos y los resultados.
Teclado: contiene los botones para operaciones, funciones y opciones adicionales.

Botones principales:

  • Números (0–9): botones amarillos para introducir valores.
  • Operaciones (+, –, ×, ÷): botones grises para realizar los cálculos.
  • Ver Pantalla: muestra el último cálculo realizado.
  • C: borra toda la pantalla.
  • <: elimina el último dígito introducido.
  • =: muestra el resultado final.
  • , (coma): se usa para escribir números decimales.
  • RC: calcula raíces cuadradas mostrando el procedimiento paso a paso.
  • |: realiza la factorización prima del número introducido.
Explicación de los botones y funciones principales de la Calculadora Alicia

3. Realiza Operaciones Básicas

Suma paso a paso explicada con la Calculadora Alicia

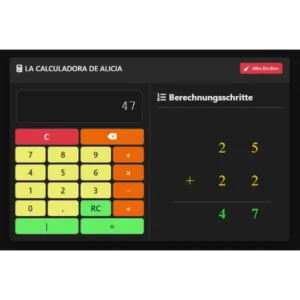
Suma

ntroduce el primer número → presiona “+” → introduce el segundo número → pulsa “=”.

Cómo restar paso a paso con la Calculadora Alicia

Resta

introduce el primer número → presiona “–” → introduce el segundo número → pulsa “=”.

Multiplicación paso a paso con la Calculadora Alicia

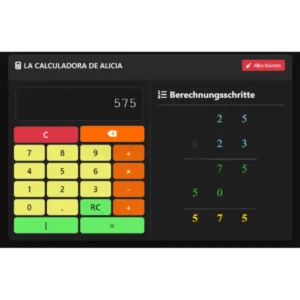
Multiplicación

introduce el primer número → presiona “×” → introduce el segundo número → pulsa “=”.

División paso a paso con explicación visual en la Calculadora Alicia

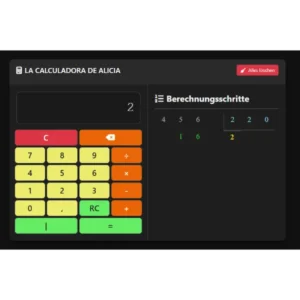
División

introduce el primer número → presiona “÷” → introduce el segundo número → pulsa “=”.

4. Borrar o Corregir Entradas

Presiona “C” para borrar todo lo que aparece en pantalla o “<” para eliminar solo el último número introducido.

5. Consultar el Último Cálculo

Haz clic en “Ver Pantalla” para revisar los cálculos anteriores y reutilizarlos sin volver a escribirlos.

6. Calcular Raíces Cuadradas

Introduce el número cuya raíz cuadrada deseas calcular y presiona “RC”.
La calculadora mostrará el resultado junto con los pasos detallados para obtenerlo, ideal para fines educativos.

Factorización prima explicada con la Calculadora Alicia

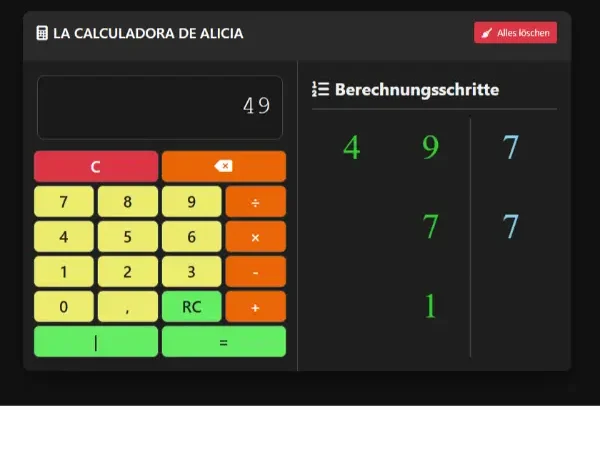
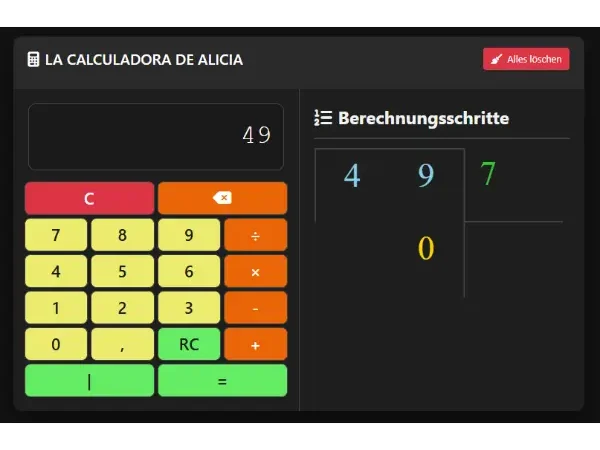
7. Calcular la Factorización Prima

Introduce un número y presiona el botón “|”.
Obtendrás su factorización en números primos con una explicación paso a paso del procedimiento.

Raíz cuadrada explicada paso a paso con la Calculadora Alicia

Ventajas de Utilizar la Calculadora Alicia

Útil en Diversos Campos

La Calculadora Alicia no está limitada al ámbito académico.
También es una herramienta práctica para profesionales de ingeniería, ciencia, física, química, estadística y economía, que requieren cálculos precisos y rápidos.
Además, puede utilizarse sin conexión al descargar la aplicación desde nuestro sitio web.

Precisión y Privacidad

Cada operación se ejecuta con máxima exactitud.
La calculadora no recopila ni comparte datos personales, garantizando total seguridad y confidencialidad en el uso.

En Constante Mejora

Nuestro equipo trabaja continuamente para mejorar y actualizar la Calculadora Alicia según las necesidades de los usuarios y los avances tecnológicos.
Puedes enviar sugerencias o ideas de nuevas funciones directamente desde la sección de contacto del sitio.

Ideal para el Aprendizaje

Más que una simple herramienta de cálculo, la Calculadora Alicia es un recurso educativo.
Sus soluciones paso a paso ayudan a comprender los procedimientos matemáticos, reforzando la lógica y el aprendizaje práctico.
Es perfecta para estudiantes que desean mejorar sus habilidades matemáticas y para docentes que buscan una herramienta didáctica eficaz.

Ventajas frente a otras calculadoras online

Frente a otras calculadoras, la calculadora Alicia destaca por su enfoque pedagógico: no solo entrega resultados, sino que enseña el procedimiento. Su privacidad (no requiere registro) y su versión web gratuita la hacen accesible. La interfaz permite alternar entre formato punto y coma para decimales, elegir modo oscuro y descargar hojas de ejercicios. Para docentes, la posibilidad de proyectar procesos paso a paso es una ventaja frente a calculadoras científicas que suelen mostrar solo el resultado final.

Divisiones con decimales y ejemplos numéricos detallados

Las divisiones con punto decimal pueden intimidar al principio. La calculadora Alicia enseña a desplazar el punto decimal en divisor y dividendo para convertir la operación en una división exacta con enteros. Ejemplo: 12,5 ÷ 0,25 → mover dos decimales en ambos para obtener 1250 ÷ 25 = 50. También se guía al usuario para hacer divisiones largas con dos cifras en el divisor, mostrando cada paso y permitiendo continuar con decimales hasta el nivel de precisión deseado.

Más ejemplos: raíces y potencias comunes

Ejemplos concretos que aparecen con frecuencia en ejercicios escolares: √9 = 3, √16 = 4, √25 = 5, √36 = 6, √49 = 7. La calculadora Alicia no solo da el resultado sino que muestra cómo comprobarlo mediante la multiplicación inversa (3×3=9). Para raíces cúbicas, por ejemplo ∛27 = 3, la herramienta muestra la descomposición en factores primos y la extracción de raíces cuando procede.

Prácticas y ejercicios recomendados

Para afianzar el aprendizaje, es esencial practicar con distintos tipos de problemas. Realiza sesiones cortas y frecuentes: diez ejercicios diarios de multiplicación, cinco de fracciones y dos de división larga. Empieza con operaciones simples y aumenta gradualmente la dificultad: sumas y restas de una cifra, multiplicaciones de dos cifras y luego fracciones o decimales.
Incluye siempre la comprobación de resultados, como multiplicar el cociente por el divisor o verificar soluciones en ecuaciones. Usa hojas imprimibles y fichas combinadas con potencias y raíces. Para niveles avanzados, añade factorización, MCM, MCD y notación científica aplicada a ejemplos reales de física o química.

Recursos para docentes y familias

Los docentes pueden incorporar la Calculadora Alicia en su planificación: ejercicios grupales, proyección de pasos en clase y tareas con hojas exportadas desde la plataforma.
Las familias pueden crear rutinas de práctica en casa, combinando juegos y ejercicios cronometrados para reforzar la motivación.
Se recomienda alternar actividades lúdicas y escritas, como tarjetas de multiplicación con temporizador. Para alumnos con dificultades, divide los problemas en pasos más pequeños y reduce la cantidad de operaciones.
Complementa con recursos digitales: videos cortos sobre procedimientos (división larga, raíces cuadradas) y listas de verificación paso a paso.

Consejos para exámenes y uso responsable de herramientas

Al usar cualquier herramienta en el estudio, es vital practicar la técnica manual antes de depender de automatismos. Para exámenes, asegúrate de conocer los métodos tradicionales: cómo hacer una división larga a mano, cómo simplificar una fracción o cómo aplicar la fórmula cuadrática. Usa la herramienta para practicar y comprobar resultados, no para sustituir el aprendizaje. Si se utiliza en clase, consulta la normativa del centro sobre el uso de calculadoras en exámenes y adapta las rutinas de estudio para reforzar la comprensión conceptual.

Conclusión

La Calculadora Alicia es una herramienta gratuita y accesible diseñada para aprender y practicar matemáticas paso a paso. Permite realizar operaciones básicas (suma, resta, multiplicación y división), trabajar con fracciones y decimales, calcular raíces y efectuar factorizaciones en primos, además de ofrecer soluciones detalladas y modo oscuro. Su enfoque didáctico y su interfaz intuitiva la hacen útil para estudiantes, docentes y familias: no solo ofrece resultados, sino que explica el proceso para reforzar la comprensión y la confianza en el aprendizaje.

Preguntas frecuentes (FAQ)

Sí, la Calculadora Alicia es completamente gratuita para la mayoría de sus funciones básicas y no requiere crear una cuenta para usarla. Algunas funciones avanzadas (como sincronización de historial entre dispositivos o espacio de almacenamiento en la nube) pueden requerir opt-in voluntario, pero el uso escolar habitual no necesita registro.

Introduce las fracciones en el modo Frac o directamente usando el teclado. La herramienta calcula el mínimo común múltiplo (m.c.m.), ajusta numeradores y muestra los pasos: conversión a denominador común, suma de numeradores, simplificación y (si procede) conversión a fracción mixta.

Escribe el número decimal (ej.: 0,75). La Calculadora Alicia indica que 0,75 = 75/100, luego simplifica ambos términos por el máximo común divisor y muestra 3/4 como resultado final, explicando cada división intermedia.

En el módulo de Regla de Tres introduce los valores conocidos. Para proporcionalidad directa aplica la proporción y muestra la fórmula paso a paso (ej.: si 4 cuadernos cuestan 10 €, ¿cuánto cuestan 7? → 10×7/4 = 17,5 €). Para proporcionalidad inversa invierte la relación y explica por qué.

Introduce dividendo y divisor y pulsa ÷, luego =. La calculadora muestra las bajadas, restos y el cociente. Si el resultado requiere decimales, te ofrece continuar la división hasta la precisión que elijas y explica el desplazamiento del punto decimal cuando corresponde.

Sí: la Calculadora Alicia permite imprimir la página con todo el procedimiento o guardarlo como PDF. También puedes exportar ejercicios y hojas imprimibles para usar en clase.

Introduce el número y pulsa la función de factorización. La herramienta dibuja el árbol de factores y lista el resultado (ej.: 78 → 2 × 3 × 13), mostrando cada división por el primo correspondiente.

Sí, admite tanto coma (estándar en español: 3,5) como punto (3.5) según la configuración del teclado o preferencia del usuario. Recomendamos usar la coma en entornos hispanohablantes para consistencia con la interfaz.

Sí. Incluye listas de ejercicios, modos para proyectar paso a paso en clase, y opciones para crear tandas de ejercicios por tema (sumas con llevadas, división larga, fracciones equivalentes, etc.).

Usa el modo Práctica para generar lotes de ejercicios (por ejemplo 5 preguntas por lote) y recibir corrección inmediata con explicación paso a paso y opción de reiniciar el quiz.

Se identifica el m.c.m. de los denominadores, se ajustan los numeradores y se resta. La Calculadora Alicia muestra la conversión, la resta de numeradores y la simplificación final, incluyendo cómo convertir el resultado a fracción mixta si procede.

Ingresa los coeficientes a, b y c. La herramienta calcula el discriminante (b² − 4ac) y según su valor usa factorización (si es posible) o la fórmula general, mostrando cada paso: cálculo del discriminante, extracción de raíces y comprobación sustituyendo las soluciones en la ecuación original.

Fracciones heterogéneas son las que tienen distinto denominador. Para operarlas, la Calculadora Alicia encuentra el denominador común (m.c.m.), convierte las fracciones y realiza la operación, mostrando la simplificación final.

Selecciona la función de logaritmos y escribe la base (si procede) y el número. La calculadora muestra la definición, el procedimiento de cálculo (cuando se usa cambio de base) y ejemplos prácticos aplicados a ejercicios científicos.

Sí. La Calculadora Alicia tiene ejercicios específicos que mezclan paréntesis, potencias/raíces, multiplicación/división y suma/resta para reforzar la jerarquía de operaciones, con explicaciones paso a paso y comprobaciones.

Introduce el número o la notación científica y la herramienta muestra la conversión (por ejemplo 5.2×10^3 = 5200) explicando el movimiento del punto decimal y el ajuste del exponente.